Komputerowe podstawy matematyki binarne, dziesiętne, heksadecimal, ósemki
- 953
- 280
- Laura Zygmunt
To, jak wyrażamy liczbę, zależy od tego, czy jesteśmy komputerem, czy człowiekiem. Jeśli jesteśmy ludźmi, prawdopodobnie wyrażamy liczby za pomocą naszego znajomego 10-bazowy system dziesiętny. Jeśli jesteśmy komputerem, prawdopodobnie u podstaw wyrażamy liczby 2-bazowy Lub dwójkowy.
Więc co jest ze wszystkimi sposobami wyrażania liczb i dlaczego one istnieją? Ten artykuł zostanie przekazany szczegółowo i mam nadzieję, że do końca będziesz liczyć na palce Octal. Co działa dobrze, o ile używasz tylko 8 palców, w końcu… Octal jest 8-bazowy.
W tym samouczku się nauczysz:
- Jak zrobić proste zliczanie w systemach nie-gruntownych, takich jak binarne, sześciokadciowskie i ośmiokątne.
- Jakie terminy 2-bazowe, 10-bazowe itp. stoją i jak je łatwiej zrozumieć.
- Związek między tymi różnymi metodami wyrażania liczb
Podstawy matematyki komputerowej: binarny, dziesiętny, sześciokadcica, ośmiorot Zastosowane wymagania i konwencje oprogramowania
| Kategoria | Wymagania, konwencje lub wersja oprogramowania |
|---|---|
| System | Niezależny od rozkładu Linuksa |
| Oprogramowanie | Wiersz poleceń Bash, system oparty na Linuksie |
| Inny | Wszelkie narzędzie, które nie jest zawarte w skorupce Bash domyślnie można zainstalować za pomocą za pomocą sudo apt-get instal instal narzędzie (Lub Mnij instalacja dla systemów opartych na Redhat) |
| Konwencje | # - Wymaga wykonywania Linux -Commands z uprawnieniami root bezpośrednio jako użytkownik root lub za pomocą sudo Komenda$-Wymaga wykonania Linux-commands jako zwykłego niepewnego użytkownika |
Dziesiętny
Wszyscy bardzo znamy system dziesiętny: 1 do 10 lub lepszy 0 do 9, sam system, o którym myśleliśmy od najwcześniejszego dnia szkoły, a nawet wcześniej przez naszych rodziców. Ale ten system liczbowy to nie wszystko. To jest po prostu jeden z nich. Nazywamy ten konkretny system 10-bazowy ponieważ ma podstawę 10 znaków, a mianowicie 0 do 9.
W dziesiętnym możemy łatwo liczyć, używając po prostu tego, co myśleliśmy: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Nie musimy w tym wysiłku, i przychodzi to naturalnie. Jeśli jednak naprawdę się nad tym zastanowić, nie ma prawdziwego logicznego związku między numerem słowa „zero” i „jeden” i „jeden” i „dwa” i tak dalej. Offcourse, z czasem to rozumiemy 0+1 = 1 I 1+1 = 2, Ale nie ma bezpośredniego prawdziwego i znaczącego Inny Połączenie między jednym a dwoma, 1 i 2. To tylko forma wyrażenia.
Aby to zilustrować, rozważ powyższe twierdzenia w porównaniu z fikcyjnym 5-bazowy system. Dla naszych umysłów jest o wiele trudniejsze, ponieważ nie zostały one przeszkolone w tym samym, do liczenia w systemie 5-bazowym. Zróbmy to nawet o krok mocniej i stwierdzić, że nasze 5 liczb są wyrażone jako (, ), +, = I . odpowiednio. Policzmy do 11, czy my?
0: (1 :) 2: + 3: = 4: . 5:) (6:)) 7 :)+ 8:) = 9:). 10: +(11: +)
Po lewej stronie mamy 10-zasadowe liczby dziesiętne, po prawej mamy nasz 5-bazowy system liczbowy liczy się w ten sam sposób (i zarówno lewa, jak i prawowa mają równe wartości numeryczne, i.mi. 10 w dziesiętnym/10-bazie jest +( W naszym 5-bazowym systemie numerycznym!).
Mogę bardzo łatwo liczyć w ten sposób, ponieważ jestem bardzo przyzwyczajony do tego baza x systemy działają. Jeśli spojrzysz nieco bliżej hrabiego, szybko odkryjesz, jak to działa i zobaczysz, jak to całkiem porównuje z naszym systemem zliczania dziesiętnego. Wskazówka jest taka; Gdy zabraknie postaci, po prostu poprzedzasz pierwszą postać z pierwszą postacią, tworząc dwie postacie. Mimo to, jak napisałbyś 100? Czy musisz pracować aż do listy? Prawdopodobne, ponieważ nasze umysły nie są wykorzystywane do wymienienia rzeczy za pomocą tych symboli.
Nasze umysły rozumieją dziesiętne i zmagają się z większością innych baza x oparte na systemach numerycznych, w których x nie ma 10. Być może przykład? Proszę obliczyć )) (((A ==-() b… (+ gdzie użyliśmy A wskazać mnożenie i B jest prosty plus. Ale nie ma w tym nic podobnego, prawda? Mimo to, jeśli przekonwertujemy to na dziesiętne i naszego znajomego + I X symbole, prawdopodobnie nie znaleźlibyśmy tych równań za ciężko.
Teraz, gdy jesteśmy uzbrojeni w zrozumienie, co baza x Naprawdę jest, reszta jest znacznie łatwiejsza. I obiecuję: nie więcej dziwnych symboli do wyrażenia liczb, to tak jest, dopóki nie dotrzemy do heksadecimal 😉
Dwójkowy
Dopóki komputery kwantowe nie uderzają w nasze lokalne sklepy komputerowe, nasze komputery są dość ograniczone. Jedyną rzeczą, w bardzo rdzeni, którą rozumie komputer moc Lub brak mocy. Nic więcej! Komputer po prostu rozumie moc lub brak mocy, ale nie "zrozumieć" Co za postać A jest lub jaka cyfra 9 Jest. Wszystkie te rzeczy i wiele więcej (ja.mi. Cały kod komputerowy) w jego bardzo rdzeniu wyraża się tak wiele zasilania lub braku mocy.
Pojedyncza taka jednostka przechowywania i ekspresji nazywa się fragment. Trochę to najbardziej niski poziom, rdzeń, magazyn komputera. A fragment może przechowywać tylko jeden 0 lub pojedynczy 1. W rzeczywistości nie może nawet przechowywać zero ani jednego, może przechowywać tylko moc (nasz 1) lub brak mocy (nasz 0). Możesz zacząć widzieć, jak działa 2-baza lub binarna: ma tylko dwa wyrażenia: 0 i 1, Brak mocy ani mocy.
Jeśli wyobrażasz to pod względem fizycznego sprzętu komputerowego, możesz wyobrazić sobie starszy napęd na dysku twardego jako płytkę pełną wielu małych miejsc, które albo mają moc (są magnetyzowane) lub nie mają zasilania (nie są magnetyzowane). Jeśli wyobrażasz to jako dane przepływające przez kabel, możesz je wyobrazić jako zasilanie lub brak zasilania.
Zróbmy więc nasze samo liczenie do 11, ale tym razem przy użyciu naszych tylko dwóch możliwych metod wyrażenia, liczb w naszym binarnym systemie numerycznym: 0 i 1.
0: 0 1: 1 2: 10 3: 11 4: 100 5: 101 6: 110 7: 111 8: 1000 9: 1001 10: 1010 11: 1011
Po lewej stronie mamy 10-zasadową dziesiętną, a po prawej mamy 2-bazowy binarny.
Kiedyś Zobacz to, Łatwo się zliczyć: po prostu zacznij od 0 i 1 i zauważ, jak 0 zawsze ma szczególne znaczenie: kiedy przychodzisz 2 W dziesiętnym 01 (I.mi. Pierwsza postać używana jako nowa lewica), ale raczej 10 ponieważ 0 ma rzeczywistą wartość zero. Innymi słowy, nie napisałbyś: 0, 1, 2, 3,…, 8, 9, 00 lub 01, ponieważ żaden nie ma sensu; jeden napisałby 10. To samo dotyczy tutaj.
To samo dotyczyło naszego 5-bazowego systemu powyżej: użyliśmy ) ( Aby wyrazić następny krok po użyciu wszystkich naszych cyfr, a nie (( co byłoby nieprawidłowe. To byłoby jak napisanie 00 zamiast 6.
Gdy znasz te podstawowe kroki, które mają zastosowanie do wszystkich systemów X-base, łatwiej jest liczyć. I możesz użyć dodawania wiodącego najwcześniejszego znaku i zresetuj właściwej prawej postaci obecnie używanej, ilekroć zabraknie Ci możliwych następnych kroków numerycznych przy użyciu tylko długości, którą masz w tej chwili. Przeczytaj kilka razy z binarnych kroków i spójrz na postęp, a wkrótce będziesz mógł liczyć na binarny, nawet bez używania palców. Jeśli używasz palców, pamiętaj o użyciu tylko dwóch.
Szesnastkowy
Więc teraz, kiedy zbadaliśmy 10-bazowe, 2-bazowe (i 5-bazowe 😉 Spójrzmy na coś, co może wydawać się dziwne na pierwszy rzut oka: 16-bazowy. Jak mielibyśmy zmieścić 16 możliwych kombinacji numerycznych do jednego znaku? Witamy w Hexadecimal, który wykorzystuje litery.
Zróbmy najpierw prostą liczbę: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f
W sumie 16 znaków, system szesnastkowy używa A-F, gdy zabraknie sposobu wyrażenia następny numer w serii. Liczenie od jednego do 11, tak jak wcześniej, byłoby tutaj dyskusyjne, ponieważ 11 jest po prostu wyrażone przez „B”. Tym razem zacznijmy nieco dalej:
0: 0 1: 1… 9: 9 10: A… 15: F 16: 10 17: 11
Po lewej stronie mamy 10-zasadową dziesiętną i po prawej mamy 16-bazową sześciokadcicę. Łatwiej jest pamiętać, pamiętaj, że Hexa-Decimal sprawia, że myślimy 6-10.
Auć! Teraz skończymy z 10 w 16-bazowej heksadecimal jest naprawdę warta 16 w 10-bazie dziesiętne! Może to być nieco mylące i od razu można zobaczyć potrzebę jasnego zrozumienia, z jakimi systemem liczbowym pracujemy, aby uniknąć kosztownych błędów.
Wiele kalkulatorów w różnych systemach operacyjnych ma ustawienie programistów lub komputerów, które można aktywować do pracy z różnymi systemami numerycznymi. Niektórzy idą o krok dalej i bardzo wyraźnie pokazują, na co dana liczba przekładaby się w różnych innych systemach numerycznych X-baz, takich jak ten świetny kalkulator zawarty w Linux Mint 20:
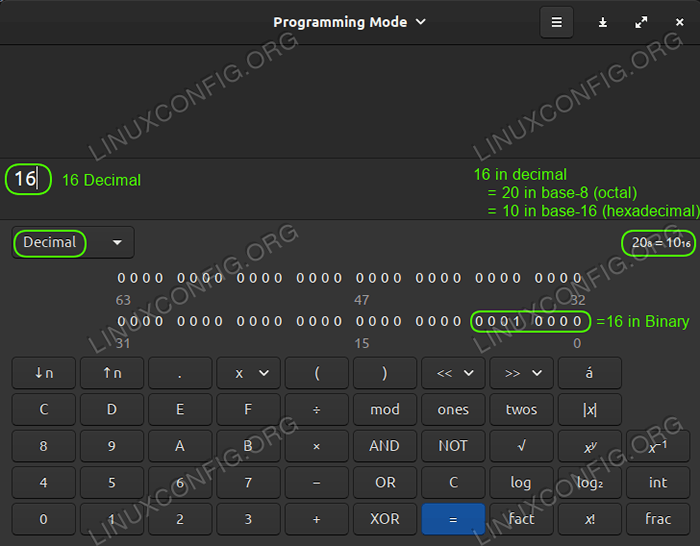Kalkulator Linux Mint 20 pokazujący dziesiętne, binarne, sześciokadcikowe, ósemkowe jednocześnie Octal
Teraz, gdy widzieliśmy poprzednie systemy numeryczne, łatwiej jest zobaczyć, w jaki sposób możemy liczyć w systemie 8-zasadowym, w tym przypadku Octal, inny system używany w połączeniu z systemami przetwarzania komputerowego i przez komputer.
W ośmiorcu mamy 8 znaków numerycznych to 0, 1, 2,…, 6, 7. Policzmy do 11 w 8-bazowym systemie numerycznym, zaczynając od 7:
7: 7 8: 10 9: 11 10: 12 11: 13
Po lewej stronie mamy 10-zasadową dziesiętną i po prawej.
Znowu widzimy nieco mylące 10 w 10-bazowej istocie dziesiętnej 12 W 8-bazowym ośmiorcu.
Dlaczego tak wiele systemów numerycznych?
Dlaczego więc jest tak wiele różnych systemów numerycznych? Powód jest prosty. Pamiętaj, jak jeden był sklepem, który umieścił binarny zero lub jeden? Cóż, jeśli weźmiesz 8 bitów, będziesz mieć jeden bajt, a bajt jest często używany do wyrażania prostych znaków alfa jednopajtowych. Jeśli myślisz o tym, jak 8 jest u podstaw tego, nie powinno to być zbyt daleko, aby zobaczyć,.
Następnie mamy heksadecimal, czyli naprawdę 2 x 8 = 16 znaków. I tutaj mamy 16 bitów (lub 2 bajtów) reprezentowanych jako jeden jeden znak. Wszystko wisi blisko siebie i naprawdę wchodzi w grę, gdy zastanawiasz się, w jaki sposób postacie alfa-numeryczne są używane i przetwarzane w systemach komputerowych. Na przykład niektóre znaki specjalne (jak na przykład japońskie lub chińskie znaki) mogą wymagać dwóch lub trzech bajtów do ich przechowywania (multi-byte).
Różne systemy numeryczne upraszczają wiele rodzajów przepływów danych, które występują w komputerze, a w zależności od przepływów, oraz wszelkich wybranych lub używanych algorytmów komputerowych, możliwe są różne optymalizacje. Większość rozwijających się języków ma na przykład wysoce zoptymalizowane przetwarzanie binarne i potencjalnie szesnastkowe oprócz przetwarzania dziesiętnego.
Wniosek
W tym artykule zleciliśmy w 2-bazowe, 10-bazowe, 16-bazowe i 8-bazowe systemy numeryczne, będąc binarnymi (2), dziesiętnym (10), szesnastkowym (16) i ośmiorodnym (8). Widzieliśmy, jakie są między nimi połączenia i jak zrobić proste liczenie we wszystkich tych systemach.
Uczenie się nieco więcej o tym, jak często działają komputery, zwłaszcza jeśli chodzi o tworzenie pierwszych programów komputerowych lub zrozumienie teorii. Kiedy ktoś staje się programistą w pełnym wymiarze godzin, na tym etapie wszystkie te systemy mają drugą naturę i są często używane w ramach rzeczywistego kodu.
Proszę, zostaw nam komentarz ze swoimi spostrzeżeniami na temat tych systemów numerycznych! A jeśli jesteś gotowy nauczyć się bardziej interesujących rzeczy, spójrz na naszą manipulację Big Data dla zabawy i zysku! Cieszyć się!
Powiązane samouczki Linux:
- Samouczek debugowania GDB dla początkujących
- Wprowadzenie do automatyzacji, narzędzi i technik Linuksa
- Rzeczy do zainstalowania na Ubuntu 20.04
- Mint 20: Lepsze niż Ubuntu i Microsoft Windows?
- Hung Linux System? Jak uciec do wiersza poleceń i…
- Rzeczy do zrobienia po zainstalowaniu Ubuntu 20.04 Focal Fossa Linux
- Jak dokonać obliczeń dziesiętnych w BASH za pomocą BC
- Mastering Bash Script Loops
- Ubuntu 20.04 Przewodnik
- Rzeczy do zrobienia po zainstalowaniu Ubuntu 22.04 JAMMY Jellyfish…