Wstęp
- 4872
- 278
- Roland Sokół
W tym szybkim samouczku dla modeli statystycznych i grafiki podamy prosty przykład regresji liniowej i dowiemy się, jak przeprowadzić tak podstawową analizę statystyczną danych. Tej analizie będą towarzyszyć przykłady graficzne, które przybędą nas do produkcji działek i wykresów z gni r. Jeśli w ogóle nie znasz korzystania z R, spójrz na samouczek wstępny: szybki samouczek na podstawowe operacje, funkcje i struktury danych.
Modele i formuły w R
Rozumiemy Model w statystykach jako zwięzły opis danych. Taka prezentacja danych jest zwykle wykazywana z Matematyczna formuła. R ma swój własny sposób reprezentowania relacji między zmiennymi. Na przykład następujący związek y = c0+C1X1+C2X2+… +CNXN+r jest w R PINET
y ~ x1+x2+…+xn,
który jest obiektem formuły.
Przykład regresji liniowej
Podajmy teraz przykład regresji liniowej dla GNU r, który składa się z dwóch części. W pierwszej części tego przykładu zbadamy związek między zwrotami indeksu finansowego denominowany w dolarie amerykańskim a tymi zwrotami denominowanymi w dolar. Dodatkowo w drugiej części przykładu dodajemy jeszcze jedną zmienną do naszej analizy, które są zwrotami indeksu denominowanymi w euro.
Prosta regresja liniowa
Pobierz przykładowy plik danych do swojego katalogu roboczego: Regresja-Example-GnU-R.CSV
Uruchommy teraz R w Linux z lokalizacji katalogu roboczego po prostu
$ R
i odczytaj dane z naszego przykładowego pliku danych:
> zwroty<-read.csv("regression-example-gnu-r.csv",header=TRUE) Możesz zobaczyć nazwy pisania zmiennych
> Nazwy (zwroty)
[1] „USA” „Kanada” „Niemcy”
Czas zdefiniować nasz model statystyczny i uruchomić regresję liniową. Można to zrobić w kilku kolejnych wierszach kodu:
> y<-returns[,1]
> x1<-returns[,2]
> zwroty.LM<-lm(formula=y~x1)
Aby wyświetlić podsumowanie analizy regresji, wykonujemy streszczenie() Funkcja na zwróconym obiekcie zwroty.LM. To jest,
> Podsumowanie (zwroty.LM)
Dzwonić:
LM (wzór = y ~ x1)
Resztki:
Min 1q mediana 3q max
-0.038044 -0.001622 0.000001 0.001631 0.050251
Współczynniki:
Oszacuj STD. Błąd T Wartość PR (> | T |)
(Przechwyty) 3.174E-05 3.862E-05 0.822 0.411
x1 9.275e-01 4.880E-03 190.062 <2e-16 ***
---
Znaczenie. Kody: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Resztkowy błąd standardowy: 0.003921 na 10332 stopnia wolności
Wiele R-kwadrat: 0.7776, dostosowany R-kwadrat: 0.7776
F-Statystyka: 3.612e+04 na 1 i 10332 df, wartość p: < 2.2e-16
Ta funkcja wyświetla powyższy odpowiedni wynik. Szacowane współczynniki są tutaj C0~ 3.174e-05 i c1 ~ 9.275e-01. Powyższe wartości p sugerują, że szacowany przechwyty C0 nie różni się znacząco od zera, dlatego można go pominąć. Drugi współczynnik różni się znacznie od zera od wartości p<2e-16. Therefore, our estimated model is represented by: y=0.93 x1. Ponadto R-Squared to 0.78, co oznacza, że około 78% wariancji zmiennej Y jest wyjaśnione przez model.
Wielokrotna regresja liniowa
Dodajmy teraz jeszcze jedną zmienną do naszego modelu i przeprowadzaj analizę regresji wielokrotnej. Pytanie brzmi teraz, czy dodanie jednej zmiennej do naszego modelu daje bardziej niezawodny model.
> x2<-returns[,3]
> zwroty.LM<-lm(formula=y~x1+x2)
> Podsumowanie (zwroty.LM)
Dzwonić:
LM (wzór = y ~ x1 + x2)
Resztki:
Min 1q mediana 3q max
-0.0244426 -0.0016599 0.0000053 0.0016889 0.0259443
Współczynniki:
Oszacuj STD. Błąd T Wartość PR (> | T |)
(Przechwyty) 2.385e-05 3.035e-05 0.786 0.432
x1 6.736e-01 4.978E-03 135.307 <2e-16 ***
x2 3.026e-01 3.783E-03 80.001 <2e-16 ***
---
Znaczenie. Kody: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Resztkowy błąd standardowy: 0.003081 na 10331 stopnia wolności
Wiele R-kwadrat: 0.8627, dostosowany R-kwadrat: 0.8626
F-Statystyka: 3.245e+04 na 2 i 10331 df, wartość p: < 2.2e-16
Powyżej możemy zobaczyć wynik analizy regresji wielokrotnej po dodaniu zmiennej x2. Ta zmienna reprezentuje zwroty z indeksu finansowego w euro. Otrzymujemy teraz bardziej niezawodny model, ponieważ skorygowany R-kwadrat wynosi 0.86, co jest większe niż wartość uzyskana przed 0.76. Zauważ, że porównaliśmy skorygowany R-kwadrat, ponieważ bierze pod uwagę liczbę wartości i wielkość próby. Ponownie współczynnik przechwytywania nie jest znaczący, dlatego szacowany model można przedstawić jako: y = 0.67x1+0.30x2.
Zwróć również uwagę, że moglibyśmy odnieść się do naszych wektorów danych według ich nazwisk, na przykład
> LM (zwraca $ USA ~ zwraca $ Kanada)
Dzwonić:
LM (formuła = zwraca $ USA ~ zwraca $ Kanada)
Współczynniki:
(Przechwyty) zwraca $ Kanada
3.174e-05 9.275e-01
Grafika
W tej sekcji pokażemy, jak używać R do wizualizacji niektórych właściwości w danych. Zilustrujemy liczby uzyskane przez takie funkcje jak działka(), boksplot (), hist (), qqnorm ().
Wykres punktowy
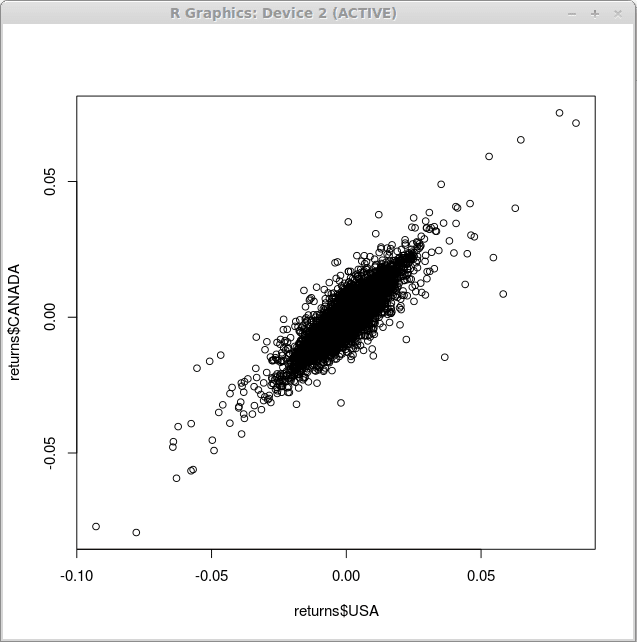
Prawdopodobnie najprostszym ze wszystkich wykresów, które można uzyskać za pomocą R, jest wykres rozproszenia. Aby zilustrować związek między denominacją dolara amerykańskiego zwrotu z indeksu finansowego a nominacją dolara kanadyjskiego działka() następująco:
> Działka (zwraca $ USA, zwraca $ Kanada)
W wyniku wykonania tej funkcji otrzymujemy schemat rozproszenia, jak pokazano poniżej

Jeden z najważniejszych argumentów, które możesz przekazać do funkcji działka() jest „typ”. Określa, jaki rodzaj wykresu należy narysować. Możliwe typy to:
• '"P„” Dla *p *maści
• '"L„” Dla *l *ines
• '"B"' dla obu
• '"C„„ For the Lines Rement of ”„ B ”''
• '"o„„ Dla obu ”*o*verpted”
• '"H„„ Dla ”*h*istogram” jak (lub „„ wysoka ”) linie pionowe
• '"S„” Dla schodów *s *teps
• '"S„” Dla innych rodzajów *s *teps
• '"N„” Brak spisku
Do nałożenia linii regresji nad powyższym schematem rozproszenia używamy krzywa() funkcja z argumentem „Dodaj” i „Col”, który określa, że linia powinna być dodana do istniejącego wykresu i koloru projektu linii odpowiednio.
> krzywa (0.93*x, -0.1,0.1, add = true, col = 2)
W związku z tym uzyskujemy następujące zmiany na naszym wykresie:
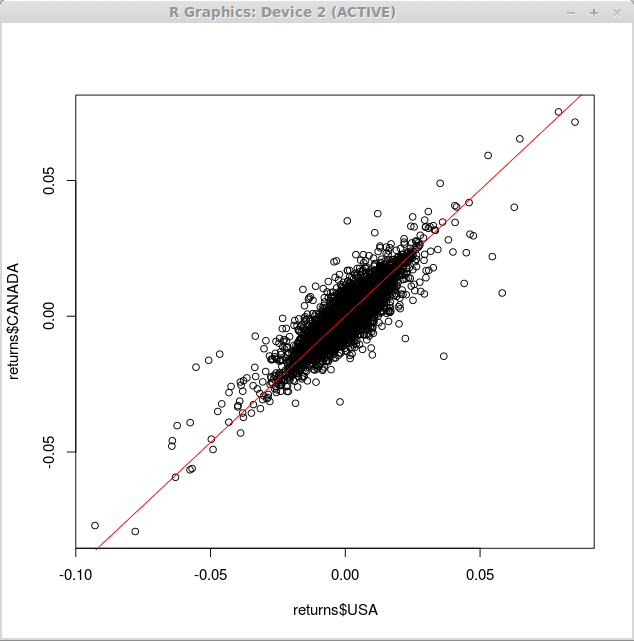
Aby uzyskać więcej informacji na temat funkcji funkcji () lub linii () użyj funkcji pomoc(), na przykład
> Pomoc (fabuła)
Wykres pudełkowy
Zobaczmy teraz, jak korzystać z boksplot () funkcja ilustrująca statystyki opisowe danych. Po pierwsze, utworzyć podsumowanie statystyk opisowych dla naszych danych przez streszczenie() funkcja, a następnie wykonać boksplot () Funkcja dla naszych zwrotów:
> Podsumowanie (zwroty)
USA Kanada Niemcy
Min. : -0.0928805 min. : -0.0792810 min. : -0.0901134
1st Q.: -0.0036463 1st Qu.: -0.0038282 1st Qu.: -0.0046976
Mediana: 0.0005977 Mediana: 0.0005318 Mediana: 0.0005021
Średnia: 0.0003897 Średnia: 0.0003859 średnia: 0.0003499
3. Qu.: 0.0046566 3rd Qu.: 0.0047591 3rd Qu.: 0.0056872
Max. : 0.0852364 Max. : 0.0752731 Max. : 0.0927688
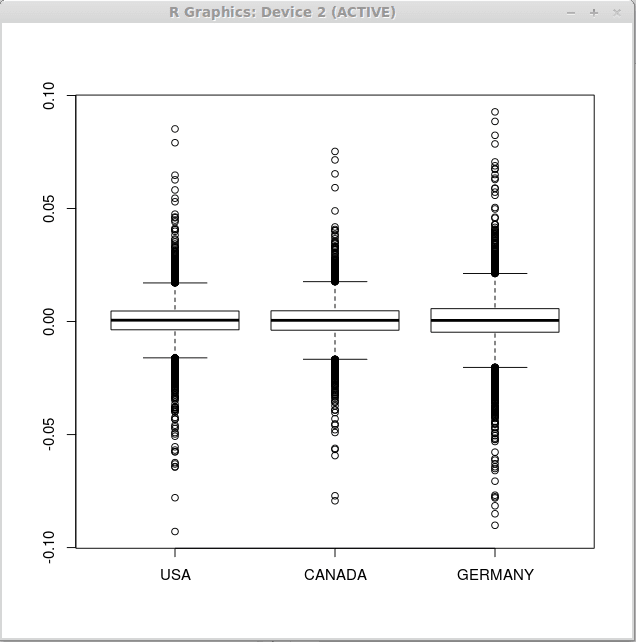
Zauważ, że statystyki opisowe są podobne dla wszystkich trzech wektorów, dlatego możemy spodziewać się podobnych wykresów dla wszystkich zestawów zwrotów finansowych. Teraz wykonaj funkcję BoxPlot () w następujący sposób
> Boxplot (zwroty)
W rezultacie otrzymujemy następujące trzy wykresy pudełkowe.
Histogram
W tej sekcji przyjrzymy się histogramom. Histogram częstotliwości został już wprowadzony we wstępie do GNU R w systemie operacyjnym Linux. Teraz wytworzymy histogram gęstości do znormalizowanych zwrotów i porównamy go z krzywą normalnej gęstości.
Najpierw normalizujmy zwroty indeksu denominowanego w dolarach amerykańskich, aby uzyskać zerową średnią i wariancję równą jednemu, aby móc porównać rzeczywiste dane z teoretyczną standardową funkcją gęstości normalnej.
> resus.norma<-(returns$USA-mean(returns$USA))/sqrt(var(returns$USA))
> wredne (retus.norma)
[1] -1.053152e-17
> var (retus.norma)
[1] 1
Teraz wytwarzamy histogram gęstości dla takich znormalizowanych zwrotów i wykreślamy standardową krzywą normalnej gęstości na takim histogramie. Można to osiągnąć poprzez następujące wyrażenie r
> Hist (retus.norma, pęknięcia = 50, freq = false)
> krzywa (dnorm (x),-10,10, add = true, col = 2)
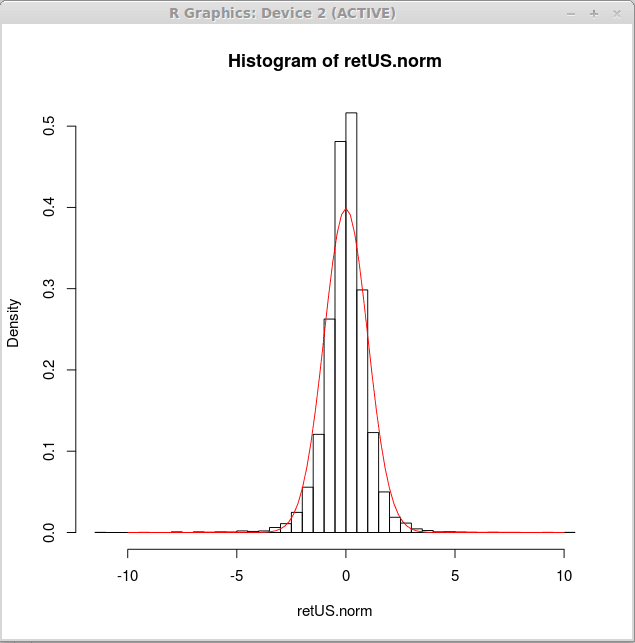
Wizualnie normalna krzywa nie pasuje do danych. Inna dystrybucja może być bardziej odpowiednia do zwrotów finansowych. Dowiemy się, jak dopasować dystrybucję do danych w późniejszych artykułach. W tej chwili możemy dojść do wniosku, że bardziej odpowiedni dystrybucja będzie bardziej wybrana na środku i będzie miał cięższe ogony.
QQ-Plot
Innym przydatnym wykresem w analizie statystycznej jest wykres QQ. Wykres QQ jest kwantylowym wykresem kwantowym, który porównuje kwantyle gęstości empirycznej z kwantylami gęstości teoretycznej. Jeśli się dobrze pasują, powinniśmy zobaczyć linię prostą. Porównajmy teraz rozkład resztek uzyskanych przez naszą analizę regresji powyżej. Najpierw uzyskamy wykres QQ dla prostej regresji liniowej, a następnie dla regresji wielokrotnej liniowej. Typ użycia QQ-Plot jest normalnym wykresem QQ, co oznacza, że kwantyle teoretyczne na wykresie odpowiadają kwantylom rozkładu normalnego.
Pierwszy wykres odpowiadający prostym resztom regresji liniowej jest uzyskiwana przez funkcję qqnorm () w następujący sposób:
> zwroty.LM<-lm(returns$US~returns$CANADA)
> qqnorm (zwroty.reszty LM $)
Odpowiedni wykres jest wyświetlany poniżej:
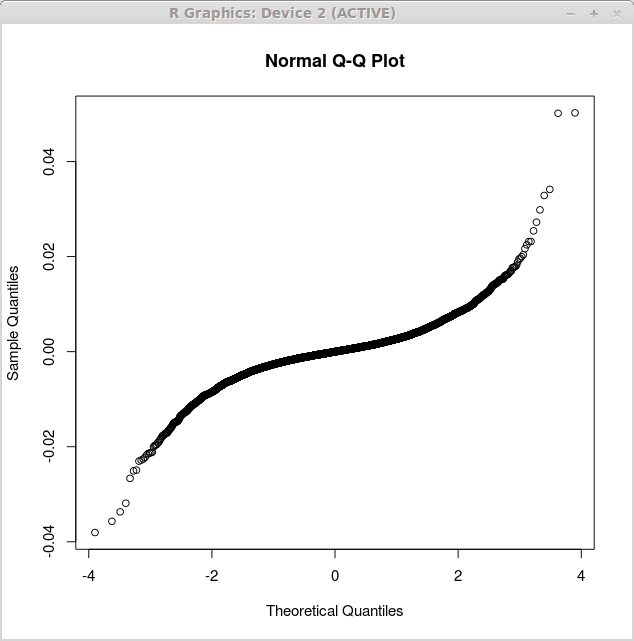
Drugi wykres odpowiada wielu resztom regresji liniowej i jest uzyskiwany jako:
> zwroty.LM<-lm(returns$US~returns$CANADA+returns$GERMANY)
> qqnorm (zwroty.reszty LM $)
Ten wykres jest wyświetlany poniżej:
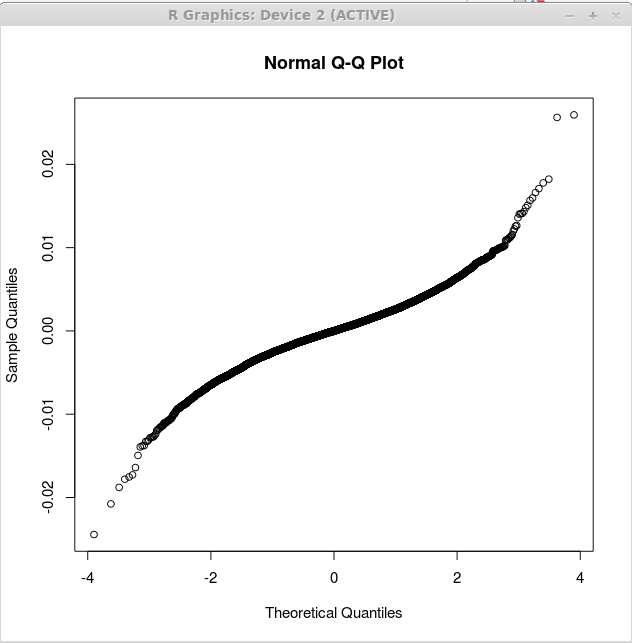
Zauważ, że drugi wykres jest bliżej linii prostej. Sugeruje to, że reszty wytwarzane przez analizę regresji wielokrotnej są bliższe normalnie rozmieszczonemu. To wspiera drugi model jako bardziej przydatny w porównaniu z pierwszym modelem regresji.
Wniosek
W tym artykule wprowadziliśmy modelowanie statystyczne z GNU r na przykład regresji liniowej. Omówiliśmy również niektóre często używane na wykresach statystycznych. Mam nadzieję, że otworzyło to drzwi do analizy statystycznej z GnU r dla Ciebie. W późniejszych artykułach omówimy bardziej złożone zastosowania R do modelowania statystycznego, a także programowania, więc czytaj dalej.
Seria samouczków GNU R:
Część I: samouczki wprowadzające: GNU R:
- Wprowadzenie do GNU R w systemie operacyjnym Linux
- Uruchamianie GNU w systemie operacyjnym Linux
- Szybki samouczek dotyczący podstawowych operacji, funkcji i struktur danych
- Szybki samouczek do modeli statystycznych i grafiki
- Jak instalować i używać pakietów w GNU r
- Budowanie podstawowych pakietów w GnU r
Część II: Język GNU:
- Przegląd języka programowania GNU
Powiązane samouczki Linux:
- Wprowadzenie do automatyzacji, narzędzi i technik Linuksa
- Rzeczy do zainstalowania na Ubuntu 20.04
- Mastering Bash Script Loops
- Rzeczy do zrobienia po zainstalowaniu Ubuntu 20.04 Focal Fossa Linux
- Zagnieżdżone pętle w skryptach Bash
- Mint 20: Lepsze niż Ubuntu i Microsoft Windows?
- Obsługa danych wejściowych użytkownika w skryptach Bash
- Ubuntu 20.04 sztuczki i rzeczy, których możesz nie wiedzieć
- Big Data Manipulacja dla zabawy i zysku Część 1
- Ubuntu 20.04 Przewodnik

